Certificacion

Prueba de hipótesis para la media, varianza y de las proporciones

Media

En vez de estimar el valor de un parámetro, a veces se debe decidir si una afirmación relativa a un parámetro es verdadera o falsa. Es decir, probar una hipótesis relativa a un parámetro. Se realiza una prueba de hipótesis cuando se desea probar una afirmación realizada acerca de un parámetro o parámetros de una población.

Una hipótesis es un enunciado acerca del valor de un parámetro (media, proporción, etc.).

Prueba de Hipótesis es un procedimiento basado en evidencia muestral (estadístico) y en la teoría de probabilidad (distribución muestral del estadístico) para determinar si una hipótesis es razonable y no debe rechazarse, o si es irrazonable y debe ser rechazada.

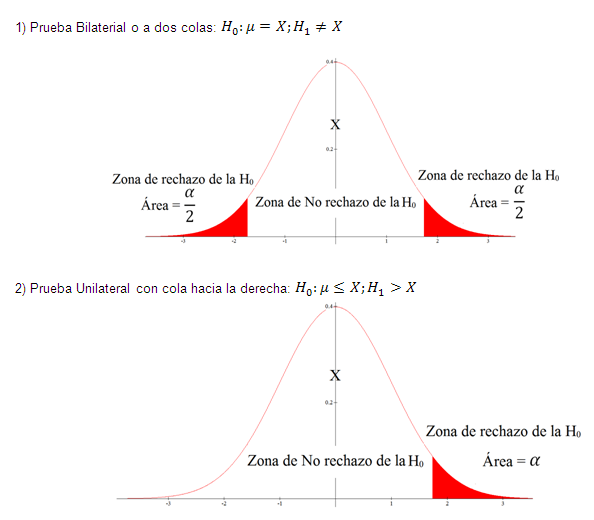
La hipótesis de que el parámetro de la población es igual a un valor determinado se conoce como hipótesis nula. Una hipótesis nula es siempre una de status quo o de no diferencia.

En toda prueba de hipótesis se presentan 3 casos de zonas críticas o llamadas también zonas de rechazo de la hipótesis nula, estos casos son los siguientes:

Varianza

Pruebas de hipótesis para una varianza Es un procedimiento para juzgar si una propiedad que se supone cumple una población estadística es compatible con lo observado en una muestra de dicha población en este caso la varianza, para ello formularemos dos Hipótesis (llamada "Hipótesis Nula") y (llamada "Hipótesis Alternativa"), con ellas realizaremos una o mas pruebas, para tratar de encontrar cual deberíamos rechazar. En este procedimiento lo que buscamos es, mediante unos criterios de rechazo preestablecidos, tratar de desmentir nuestra “Hipótesis Nula” por lo cual tomaríamos la “Hipótesis alternativa”, de lo contrario no rechazaríamos nuestra ”Hipótesis Nula” y desecharíamos la ”Hipótesis 

Proporción 

Las pruebas de proporciones son adecuadas cuando los datos que se están analizando constan de cuentas o frecuencias de elementos de dos o más clases. El objetivo de estas pruebas es evaluar las afirmaciones con respecto a una proporción (o Porcentaje) de población. Las pruebas se basan en la premisa de que una proporción muestral (es decir, x ocurrencias en n observaciones, o x/n) será igual a la proporción verdadera de la población si se toman márgenes o tolerancias para la variabilidad muestral. Las pruebas suelen enfocarse en la diferencia entre un número esperado de ocurrencias, suponiendo que una afirmación es verdadera, y el número observado realmente. La diferencia se compara con la variabilidad prescrita mediante una distribución de muestreo que tiene como base el supuesto de que  es realmente verdadera.

En muchos aspectos, las pruebas de proporciones se parecen a las pruebas de medias, excepto que, en el caso de las primeras, los datos muestrales se consideran como cuentas en lugar de como mediciones. Por ejemplo, las pruebas para medias y proporciones se pueden utilizar para evaluar afirmaciones con respecto a:

1) Un parámetro de población único (prueba de una muestra)

2) La igualdad de parámetros de dos poblaciones (prueba de dos muestras), y

3) La igualdad de parámetros de más de dos poblaciones (prueba de k muestras). Además, para tamaños grandes de muestras, la distribución de muestreo adecuada para pruebas de proporciones de una y dos muestras es aproximadamente normal, justo como sucede en el caso de pruebas de medias de una y dos muestras.

intervalo de confianza para la varianza de distribución normal

Dada una variable aleatoria con distribución Normal N(μ; σ), el objetivo es la construcción de un intervalo de confianza para el parámetro σ, basado en una muestra de tamaño n de la variable. 

A partir del estadístico

la fórmula para el intervalo de confianza, con nivel de confianza 1 − α es la siguiente

Donde χ²_α/2 es el valor de una distribución ji-cuadrado con n − 1 grados de libertad que deja a su derecha una probabilidad de α/2.

Por ejemplo, dados los datos siguientes:

• Distribución poblacional: Normal
• Tamaño de muestra: 10
• Confianza deseada para el intervalo: 95 %
• Varianza muestral corregida: 38,5

Un intervalo de confianza al 95 % para la varianza de la distribución viene dado por:

que resulta, finalmente

intervalo de confianza para las proporciones

Dada una variable aleatoria con distribución Binomial B(n, p), el objetivo es la construcción de un intervalo de confianza para el parámetro p, basada en una observación de la variable que ha dado como valor x. El mismo caso se aplica si estudiamos una Binomial B(1, p) y consideramos el número de veces que ocurre el suceso que define la variable al repetir el experimento n veces en condiciones de independencia.

Existen dos alternativas a la hora de construir un intervalo de confianza para p:

• Considerar la aproximación asintótica de la distribución Binomial en la distribución Normal.
• Utilizar un método exacto.

Aproximación asintótica

Tiene la ventaja de la simplicidad en la expresión y en los cálculos, y es la más referenciada en la mayoría de textos de estadística. Se basa en la aproximación

que, trasladada a la frecuencia relativa, resulta

Tomando como estadístico pivote

 

que sigue una distribución N(0, 1), y añadiendo una corrección por continuidad al pasar de una variable discreta a una continua, se obtiene el intervalo de confianza asintótico:

donde z_α/2 es el valor de una distribución Normal estándar que deja a su derecha una probabilidad de α/2 para un intervalo de confianza de  (1 − α) · 100 %. Las condiciones generalmente aceptadas para considerar válida la aproximación asintótica anterior son:

El intervalo obtenido es un intervalo asintótico y por tanto condicionado a la validez de la aproximación utilizada. Una información más general sobre los intervalos de confianza asintóticos puede encontrase aquí.

Intervalo exacto

Aun cuando las condiciones anteriores no se verifiquen, es posible la construcción de un intervalo exacto, válido siempre pero algo más complicado en los cálculos. Es posible demostrar que un intervalo exacto para el parámetro p viene dado por los valores siguientes:

intervalos de confianza para la diferencia de medias

Supondremos la existencia de dos poblaciones sobre las que una variable determinada sigue una distribución Normal con idéntica varianza en las dos. Sobre la población 1, la variable sigue una distribución N(µ₁, σ) y, sobre la población 2, sigue una distribución N(µ₂, σ). Igualmente supondremos que disponemos de dos muestras aleatorias independientes, una para cada población, de tamaños muestrales n₁ y n₂ respectivamente.

El objetivo es construir un intervalo de confianza, con nivel de confianza (1 − α) · 100 %, para la diferencia de medias

µ₁ − µ₂

El método se basa en la construcción de una nueva variable D, definida como la diferencia de las medias muestrales para cada población

Esta variable, bajo la hipótesis de independencia de las muestras, sigue una distribución Normal de esperanza

µ₁ − µ₂

y de varianza

La estimación conjunta, a partir de las dos muestras, de la varianza común viene dada por la expresión

y, utilizando la propiedad de que la variable

sigue una distribución χ² con n₁ + n₂ − 2 grados de libertad, podemos construir un estadístico pivote que siga una distribución t de Student y que nos proporciona la fórmula siguiente para el intervalo de confianza para la diferencia de medias:

donde t_α/2 es el valor de una distribución t de Student con n₁ + n₂ − 2 grados de libertad que deja a su derecha una probabilidad de α/2.

Estimadores

En estadística, un estimador es estadístico(esto es, una función de la muestra) usado para estimar un parámetro desconocido de la población. Por ejemplo, si se desea conocer el precio medio de un artículo (el parámetro desconocido) se recogerán observaciones del precio de dicho artículo en diversos establecimientos (la muestra) y la media aritmética de las observaciones puede utilizarse como estimador del precio medio.

un

Para cada parámetro pueden existir varios estimadores diferentes. En general, escogeremos el estimador que posea mejores propiedades que los restantes, como insesgadez, eficiencia, convergencia y robustez(consistencia).

Distribución de Varianzas

Imprimir

INSTITUTO TECNOLOGICO DE CHIHUAHUA

<<   Contenido   >>

DISTRIBUCION JI-CUADRADA (X²)

En realidad la distribución ji-cuadrada es la distribución muestral de s². O sea que si se extraen todas las muestras posibles de una población normal y a cada muestr

a se le calcula su varianza, se obtendrá la distribución muestral de varianzas.

Para estimar la varianza poblacional o la desviación estándar, se necesita conocer el estadístico X². Si se elige una muestra de tamaño n de una población normal con varianza , el estadístico:

tiene una distribución muestral que es una distribución ji-cuadrada con gl=n-1 grados de libertad y se denota X² (X es la minúscula de la letra griega ji). El estadístico ji-cuadrada esta dado por:

donde n es el tamaño de la muestra, s² la varianza muestral y  la varianza de la población de donde se extrajo la muestra. El estadístico ji-cuadrada también se puede dar con la siguiente expresión: